- Information
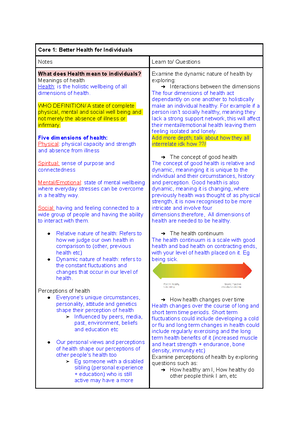
- AI Chat
Was this document helpful?
Sgtaweek 9 solution
Subject: Statistical Mathematics
4 Documents
Students shared 4 documents in this course
Was this document helpful?

Linear Regression – Part 2 © Copyright Macquarie University 2020 1
Linear Regression – Part 2
In this exercise we will:
Use Excel output to assess the relationship between two numerical variables.
Use the coefficient of determination to measure the proportion of variation in the
dependent variable that is explained by the independent variable.
Use the correlation coefficient to measure the strength and direction of the linear
relationship between two numerical variables.
Use the equation of the Least Squares Regression line to make predictions.
Research Question: Is there a relationship between BMI and systolic blood pressure?
Systolic blood pressure is a measure of the amount of pressure in the arteries during the
contraction of the heart muscle. The Body Mass Index (BMI) in kg/m2 and systolic blood
pressure in mmHg were measured for a sample of 22 adult males between the ages of 30
and 45 years. Output from the regression analysis in Excel is given below:
SUMMARY OUTPUT
Regression Statistics
Multiple R 0.60469
R Square 0.36566
Adjusted R Square 0.33394
Standard Error 6.87323
Observations 22
ANOVA
df SS MS F Significance F
Regression 1 544.6274281 544.6274281 11.52861551 0.002871778
Residual 20 944.8271173 47.24135587
Total 21 1489.454545
Coefficients Standard Error t Stat P-value Lower 95% Upper 95%
Intercept 74.22500769 15.47881821 4.795263223 0.000110208 41.93675871 106.5132567
BMI 2.171245908 0.639470383 3.395381498 0.002871778 0.837334063 3.505157753