- Information
- AI Chat
Laplace transforms to solve linear differential equations
Process Control Systems 3B
Durban University of Technology
Preview text
Laplace transforms to solve linear differential equations The application of Laplace transforms to the solution of linear differential equations is of major importance in linear control system problems. An equation of the form Lldf(t) kpdPg(t)Kldg(t) Lof(t) dt dtn dt is called a differential equation. It consists of one independent variable (t), one or more dependent variables g(t) and f(t) and one or more derivatives. 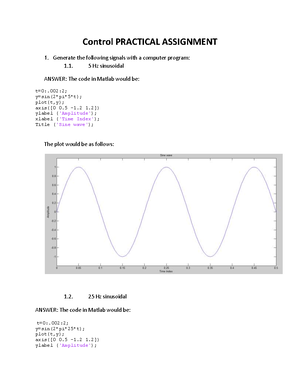10 Use Laplace to solve the following differential equation and plot the response as a function of time: fl (t) 3f(t) 2 with 2 and fl (t) the first derivative of f(t). Laplace transform: 2 sF(s) 3F(s) s 2 sF(s) 2 3 F(s) s1 s Thus 1 1 3s(ts l) where 1 is the time constant 3 Inverse Laplace transform: 1 l E I (RAVEN Table 5, page 173) For certain values oft, the function f(t) can be plotted as shown in Fig. 3. o,1759 0,2589 0,2985 t 1 f(l) 0,3167 t 2 f(2) 0,3325 f(3) Figure 3 2 3 3.3 Transfer function definition The transfer function of a control system component is defined as the ratio of the Laplace transform of the output to the Laplace transform of the input of the component, assuming the initial conditions to be zero. g(t) INPUTOUTPUT f(t) LAPLACE TRANSFORMATION INPUT OUTPUT TRANSFER FUNCTION Figure 3 The input and output of the system in Fig. 3, is assumed to be related the differential equation, (3), whose coefficients are constant. The Laplace transform of the above mentioned equation, is given : KO Lnsn and the transfer function G(s), is the ratio assuming that the initial conditions are zero. The transfer function is not dependant on the excitation and initial conditions, for it is a property of the system components only. The numerator of the transfer function can be factored in the form
Laplace transforms to solve linear differential equations
Course: Process Control Systems 3B
University: Durban University of Technology
