- Information
- AI Chat
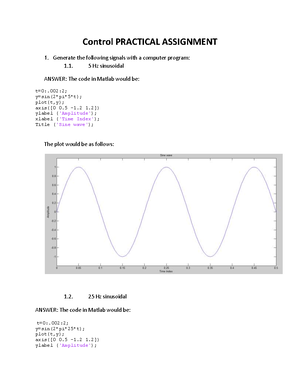
Means OF Partial Fractions
Process Control Systems 3B
Durban University of Technology
Preview text
Warning: TT: undefined function: 32 Warning: TT: undefined function: 32
MEANS OF PARTIAL FRACTIONS,
Inverting yields for the response
no (t) = (1 -4e 3t +3e )u (Table B. 1, APPENDIX B)
Note that as time approaches infinity, no Because no = nin for steady-state operation, the
coefficient of the v = nin term in Equation (4) [Text book] must be unity. This fact is
substantiated by Equation (4) [Text book], which describes the steady-state behaviour of
this system.
(b) Response of this system when all initial conditions
are zero, and u is a step function of constant value
u, and nin = 0.
u For Nin(s) = O and — the transformed equation is:
s
u (6)
AGAIN THIS EQUATION IS OBTAINED BY MEANS OF PARTIAL
FRACTIONS
Inverting yields for the response:
no (t) — (Table B. 1, APPENDIX B)
For steady-state operation, no = -5u. As is verified by Equation (4), the coefficient of the u term is -5.
The steady-state behaviour does not depend on the values of and T2, but the transient 1 behaviour does. For example, if =and — , the transformed equation becomes 15 2
(7)
n For Nin (s) =
s
and U(s) = 0, the preceding becomes:
n (8)
Inverting yields for the response:
-12t n
For Nin (s) = 0
u and U(s) — S
Equation (7) becomes:
u (9)
Inverting yields for the response:
-12t u
NOTE: See different partial fraction techniques, paragraph 3.
Example 6
Ref. RAVEN example 5, page 188.
See question in text book.
Solution
Response ofthe system to a unit step change in the input x. From the open-loop system, Fig. (5) [Text book], the equation relating the output y to the input x is:
K 1
x [K = I and (given)]
1+tD 1+51)
i. Y + 5Dy = x
thus
5
Transforming each term yields for the Laplace transform
sY(s) - y(0) + =
For y(0) = O (initial conditions are zero)
(1)
and
(unit step change in the input x)
5
s
then Equation (1) becomes
(partial-fraction expansion)
Inverting yields for the response
(Table B l , APPENDIX B)
This result shows that the time constant is 5 and the steady-state gain is 1.
-o,2t
i.
i. x
Therefore the equation relating the output y to the input x is:
x (1)
To decrease the time constant by a factor of 10, then 1 + KIK2 =10. To maintain the same steady-state gain of l ,
Hence
From the relationship 1 +KlK2 =1 +10K2 = 10, it follows that K2 0,9.
Response ofthis system to a unit step change in the input x. Substitute the values of Kl and K2 into Equation (1), the resulting input-output equation is: 1 x 1 + o,5D
or Dy + 2y = 2x
Transforming each term yields for the Laplace transform: sY(s) - y(0) + 2Y(s) = 2X(s)
For y(0) = 0 (initial conditions are zero)
2X(s) (2)
1 and X(s) = (unit step change), then Equation (2) becomes s
2 1 1
(partial-fraction expansion)
Inverting yields for the response -t/0,
This result shows that the time constant — 0,5 has been reduced by a factor of 10 and the steady-
state gain remains 1.
The partial-fraction expansion constants are:
— 214 -
Thus
3 4 1
Inverting yields for the response:
c(t) = 3e-t - 4e 2t + e
The derivative is:
t 8e-2t - 3 e
Substitution oft = 0+ into the preceding expressions shows that c(0+) 0 and c' (0+) -2.
These values may also be verified by application of the initial-value theorem.
c(0+) = S = 00
c l (0+) = limsL[c l = s[sC(s) —
Note that the initial value c l (0) = 0 at time t = 0- is different from the value c l (0+) at time t = 0+. Thus, this problem could not be solved by classical methods.
Example 9
Example 12
For the second-order system shown in Fig. 3, of which the transfer function is given by:
9 s 2
+3s+
Determine the following transient response characteristics for a unit-step input:
peak time tp;
the percentage overshoot (PO), and
rise time tr.
the settling time, ts
Solution
1. Peak time tp
Figure 3.
The closed-loop transfer ftmction, T(s), is given by ( See Chapter 2, paragraph 2.12).
The denominator of the closed-loop transfer function does not have real roots.
Thus s 2 + 3s + 18 = s 2 + 2Cons - Fon
2
9
therefore (1)
From equation (1), the undamped natural frequency (on) and the damping ratio (C), can be
determined.
on = 4,24 rad/s c = 0,
The damped natural frequency (Od), is then:
4,24 1 -0,354 2
= 3,965 rad/ s
The peak time is then:
tP
3,
= 0,792 sec
2. Percentage overshoot
PO = exp x 100%
Thus
c(t) (2)
The steady-state value is thus 0,5.
Suppose ti is the time taken for the response to reach 10 % of the steady-state value.
(See Fig.3).
Thus
10
c(tl )
10
= 0,05 units
Now, equation (2) becomes:
0 05 — — 2
Therefore ti = 0, 113 sec
Suppose t2 is the time taken for the response to reach 90 % of the steady-state value, 1.
(Again: See Fig. 3).
Thus
90
100
2
Means OF Partial Fractions
Course: Process Control Systems 3B
University: Durban University of Technology
- Discover more from:
