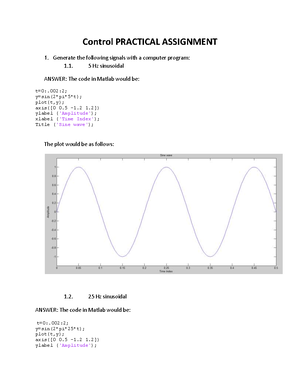
- Information
- AI Chat
Series and parallel laws
Process Control Systems 3B
Durban University of Technology
Preview text
Series and parallel laws
Elements are usually connected in either a series or a parallel arrangement. Arriving at the equation for such systems can be greatly simplified by the use of the laws for series and for parallel combinations.
Series electric circuits
A general serie circuit is shown in Fig. 2(a). In a series circuit, the total voltage drop E is the sum of the individual voltage drops across each element, and the same current I flows through each element.
(a)
1
z
1
(b)
Figure 2.
The equation for the summation of the voltage drop is:
E = ER + EL + Ec from paragraph 2 (text book).
i.
E = —+—fldt+ f Idt
2
therefore
RI +R2 +LlD+L2D+ 1
d 1 dt D
The equation relating the voltage E and current I for any electric circuit can be expressed in the form
where Z is the impedance for the circuit, E is the voltage drop across the circuit, and I is the total current flowing through the circuit. For the case of equation (2) the impedance
1
z=Rl +R2 +LlD+L2D+ CID C2D
The block-diagram representation for this system is shown in Fig. 2(b)
Parallel circuits
A general combination of electrical elements in parallel is shown in Fig. 2(a). The distinguish features of a parallel arrangement are that the voltage drop E across each element
dt
The impedance Z = (LID) (L2D) RI R 2
For elements in parallel, the total impedance is equal to 1 divided by the sum of the reciprocal of the impedance of each element. The block-diagram representation is shown in Fig. 2(b)
Series mechanical elements
Ref. RAVEN, page 26. A series of mechanical elements is shown in Fig. 2(a). In general, it is better to use the
equivalent "grounded chair" for a mass as shown in Fig 2(b), rather than the more common representation of Fig. 2(a). The fact that the mass is in series with the other elements is more readily seen from Fig. 2(b) than from Fig. 2(a). In determining the inertial force, the acceleration of a mass is always taken with respect to ground. Thus providing the grounded chair to indicate motion relative to the ground is a more justifiable representation than Fig.
2(a) which better the actual physical arrangement of the elements in the system. For series mechanical elements, the force f is equal to the summation of the forces acting on each individual component, and each element undergoes the same displacement.
Note: The principle "grounded chair" will be discussed in full detail in the next
section.
+ CID C 21)
(a) x
(c)
Figure 2.
(b)
Draw co-ordinates such that the co-ordinate at which the force acts is at the top and ground is at the bottom.
Insert each element in its correct orientation with respect to these co-ordinates.
Consider the coupled mass-spring-damper system shown in Fig. 2 (a)
(a)
x
(b) (c)
Figure 2.
The co-ordinates for this system are x and y and ground. Draw the co-ordinates as shown in
Fig. 2 (b). ( Step 1 above). To do step 2, we must note that for the spring Kl and mass Ml the co-ordinates are x and ground; for the spring K and the damper B the co-ordinates are x and y; and finally for mass M2 and f spring the co-ordinates are y and ground. Inserting these elements between the proper co-ordinates as shown in Fig. 2(c) completes the grounded-chair representation. The series and parallel
combinations are now recognised directly from this groundedchair representation. The equation for the force f is:
x (2)
- Consider the dynamic vibration absorber shown in Fig. 2 (a). The grounded-chair representation is shown in Fig. 2 (b). The co-ordinate x at which the force f acts is drawn at the top, and the ground is at the bottom. The co-ordinates for Ml, Kl and B are x and ground; for K2 the co-ordinates are x and y; and finally for M2 the coordinates are y and ground.
Now the equation for the force f is:
f = MID 2 +BD+KI + x (2)
(a)
(b)
Figure 2: Dynamic vibration absorber
2.8 Thermal systems
Ref. RAVEN page 38, paragraph 2.
Series and parallel laws
Course: Process Control Systems 3B
University: Durban University of Technology

- Discover more from: