- Information
- AI Chat
Limbas-Lesson Plan - This lesson plan is a 7Es semi-detailed. It's all about the Introduction of
BSEd Mathematics (HOM-1)
JH Cerilles State College
Recommended for you
Preview text
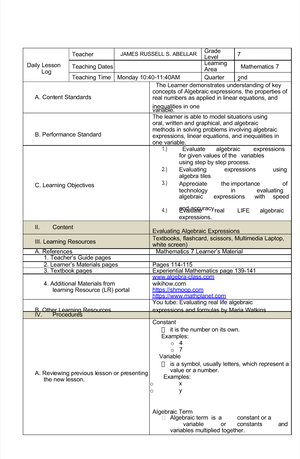
J. CERILLES STATE COLLEGE
Mati, San Miguel, Zamboanga del Sur School of Teacher Education
Teacher Angel P. Limbas Grade & Section Grade 7 Date & Time
July 20, 2050 9:45-10:45 AM
Learning Area Mathematics
A. Content Standards
Demonstrates the introduction of set, elements and cardinality. B. Performance Standards
The learners will be able to describe well- defined sets, subsets, universal sets, and cardinality. C. Learning Competency
At the end of the lesson, the learners will be able to: 1. Defined sets, elements of sets and cardinality. 2. Describe and illustrate well-defined sets and null sets. 3. Determine the element/s of given set. 4. Identify the number of elements or its cardinality.
I. CONTENT Introduction of sets, elements and cardinality. II. LEARNING RESOURCES A. References
B. Materials C. Other Learning Resource
7 Mathematics: Quarter 1: Introduction of sets Laptop, Projector, Marker, Manila Paper, Pen, and Printed materials Books Internet
III. PROCEDURES TEACHER’S ACTIVITY (5 minutes)
Prayer
Greetings
Energizer
Checking of Attendance
Class Management
The teacher asks a student to lead the prayer. The Teacher greets the students. The teacher gives an energizer called “minions dance”. youtu/OQnVSQoxL The teacher checks the attendance. Directions: the student will say there favorite foods or draw every time they here their name called. The teacher reminds the students about the classroom rules. 1. Treat others with respect. 2. Listen to the teacher when she speaks. 3. Listen and follow directions.
- Raise your hand before speaking or leaving your seat..
A. Reviewing Previous Lesson
ELICIT (3 minutes)
In this part, the teacher will ask to recall what they have learned in grade 6 mathematics. Review Questions: 1. What have learned in your last year mathematics? 2. Is the mathematics fun? 3. What part of math are you good at?
B. Establishing A Purpose for The Lesson
ENGAGE (5 minutes)
The teacher will give a challenge and entertaining activity called “complete me”.
Guidelines: The teacher put a numbers that not complete, then the students get a number in a box to put in blank that they think is the missing number that complete it.
Task 1: {1, 2 ,3, __ , __, 6, 7, 8, 9} Task 2: {2, 4, 6, __, 10, 12, __} Task 3: {3, 5, __, 9, __, __, __} Task 4: {1, 4, 9, __, , 36} Task 5: {5,10,, 20, 25, __}
C. Presenting Examples/Insta nces of The New Lesson
Answer: 1. 4 and 5 2. 8 and 14 3. 7, 11, 13, and 15 4. 16 and 25 5. 15 and 30
D. Discussing New Concepts and Skills #
EXPLORE (2 minutes)
The teacher will introduce the topic “introduction of sets” and will be asking the students if they have an idea. The students who participate will be given a “chocolate candy or any foods available, depends upon the teacher ”.
E. Discussing New Concepts and Practicing New Skills #
F. Developing Mastery
EXPLAIN (20 minutes)
The teacher will ask the students to read the Learning Objectives:
the above example, 2 ∈ A. If an element is not a member of a set, then it is denoted using the symbol '∉'. For example, 3 ∉ A.
Cardinal Number of a Set
The cardinal number, cardinality, or order of a set denotes the total number of elements in the set. For natural even numbers less than 10, n(A) = 4. Sets are defined as a collection of unique elements. One important condition to define a set is that all the elements of a set should be related to each other and share a common property. For example, if we define a set with the elements as the names of months in a year, then we can say that all the elements of the set are the months of the year. Representation of Sets in Set Theory
There are different set notations used for the representation of sets in set theory. They differ in the way in which the elements are listed. The three set notations used for representing sets are: Semantic form Roster form Set builder form
Let us understand each of these forms with an example.
Set of first five even natural numbers Semantic Form Roster Form Set Builder Form A set of first five even natural numbers
{2, 4, 6, 8, 10} {x ∈ ℕ | x ≤ 10 and x is even}
Semantic Form
Semantic notation describes a statement to show what are the elements of a set. For example, a set of the first five odd numbers.
Roster Form
The most common form used to represent sets is the roster notation in which the elements of the sets are
enclosed in curly brackets separated by commas. For example, Set B = {2,4,6,8,10}, which is the collection of the first five even numbers. In a roster form, the order of the elements of the set does not matter, for example, the set of the first five even numbers can also be defined as {2,6,8,10,4}. Also, if there is an endless list of elements in a set, then they are defined using a series of dots at the end of the last element. For example, infinite sets are represented as, X = {1, 2, 3, 4, 5 ...}, where X is the set of natural numbers. To sum up the notation of the roster form, please take a look at the examples below.
Finite Roster Notation of Sets : Set A = {1, 2, 3, 4, 5} (The first five natural numbers)
Infinite Roster Notation of Sets : Set B = {5, 10, 15, 20 ....} (The multiples of 5)
Set Builder Form
The set builder notation has a certain rule or a statement that specifically describes the common feature of all the elements of a set. The set builder form uses a vertical bar in its representation, with a text describing the character of the elements of the set. For example, A = { k | k is an even number, k ≤ 20}. The statement says, all the elements of set A are even numbers that are less than or equal to 20. Sometimes a ":" is used in the place of the "|".
Visual Representation of Sets Using Venn Diagram
Venn Diagram is a pictorial representation of sets, with each set represented as a circle. The elements of a set are present inside the circles. Sometimes a rectangle encloses the circles, which represents the universal set. The Venn diagram represents how the given sets are related to each other.
youtu/v_U7ERmMGzU
Types of Sets
There are different types of sets in set theory. Some of these are singleton, finite, infinite, empty, etc.
Singleton Sets
A set that has only one element is called a singleton set or also called a unit set. Example, Set A = { k | k is an integer between 3 and 5} which is A = {4}.
Finite Sets
As the name implies, a set with a finite or countable number of elements is called a finite set. Example, Set B = {k | k is a prime number less than 20}, which is B = {2,3,5,7,11,13,17,19}
Infinite Sets
A set with an infinite number of elements is called an infinite set. Example: Set C = {Multiples of 3}.
Empty or Null Sets
A set that does not contain any element is called an empty set or a null set. An empty set is denoted using the symbol '∅'. It is read as 'phi'. Example: Set X = { }.
Equal Sets
If two sets have the same elements in them, then they are called equal sets. Example: A = {1,2,3} and B = {1,2,3}. Here, set A and set B are equal sets. This can be represented as A = B.
Unequal Sets
If two sets have at least one different element, then they are unequal sets. Example: A = {1,2,3} and B = {2,3,4}. Here, set A and set B are unequal sets. This can be represented as A ≠ B.
Equivalent Sets
Two sets are said to be equivalent sets when they have the same number of elements, though the elements are
different. Example: A = {1,2,3,4} and B = {a,b,c,d}. Here, set A and set B are equivalent sets since n(A) = n(B)
Overlapping Sets
Two sets are said to be overlapping if at least one element from set A is present in set B. Example: A = {2,4,6} B = {4,8,10}. Here, element 4 is present in set A as well as in set B. Therefore, A and B are overlapping sets.
Disjoint Sets
Two sets are disjoint if there are no common elements in both sets. Example: A = {1,2,3,4} B = {5,6,7,8}. Here, set A and set B are disjoint sets.
Subset and Superset
For two sets A and B, if every element in set A is present in set B, then set A is a subset of set B(A ⊆ B) and in this case, B is the superset of set A(B ⊇ A). Example: Consider the sets A = {1,2,3} and B = {1,2,3,4,5,6}. Here:
A ⊆ B, since all the elements in set A are present in set B. B ⊇ A denotes that set B is the superset of set A.
Universal Set
A universal set is the collection of all the elements regarding a particular subject. The universal set is denoted by the letter 'U'. Example: Let U = {The list of all road transport vehicles}. Here, a set of cars is a subset for this universal set, the set of cycles, trains are all subsets of this universal set.
Power Sets
Power set is the set of all subsets that a set could contain. Example: Set A = {1,2,3}. Power set of A is = {∅, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}. Operations on Sets
Some important operations on sets in set theory include union, intersection, difference, the complement of a set,
In the above figure, the shaded portions in "blue" show the set that they are labelled with. Sets Formulas in Set Theory
Sets find their application in the field of algebra, statistics, and probability. There are some important set theory formulas in set theory as listed below.
For any two overlapping sets A and B,
n(A U B) = n(A) + n(B) - n(A ∩ B) n (A ∩ B) = n(A) + n(B) - n(A U B) n(A) = n(A U B) + n(A ∩ B) - n(B) n(B) = n(A U B) + n(A ∩ B) - n(A) n(A - B) = n(A U B) - n(B) n(A - B) = n(A) - n(A ∩ B)
For any two sets A and B that are disjoint,
n(A U B) = n(A) + n(B) A ∩ B = ∅ n(A - B) = n(A) Properties of Sets
Similar to numbers, sets also have properties like associative property, commutative property, and so on.
There are six important properties of sets. Given, three sets A, B, and C, the properties for these sets are as follows.
- Finding Practical Applications of Concepts and Skills in Daily Living
- Making Generalizations and Abstractions About the Lesson
Answers:
- Solution: a) Set A = {7,14,21,28,35,42,49, 56}. These are the first 8 multiples of 7. Since there are 8 elements in the set, cardinal number n (A)
ELABORATE (15 minutes)
In summary, ets in mathematics, are simply a collection of distinct objects forming a group. A set can have any group of items, be it a collection of numbers, days of a week, types of vehicles, and so on. Every item in the set is called an element of the set. Curly brackets are used while writing a set. A very simple example of a set would be like this. Set A = {1, 2, 3, 4, 5}. In set theory, there are various notations to represent elements of a set. Sets are usually represented using a roster form or a set builder form. The teacher will group the students into three groups for the activity. Mechanics: Each group will be given a manila paper and a marker to write solutions and answers in manila paper. After that, they will present their answer in the class, each group have their representative to explain their output. Questions: 1. Find the elements of the sets represented as follows and write the cardinal number of each set. a) Set A is the first 8 multiples of 7 b) Set B = {a,e,i,o,u} c) Set C = {x | x are even numbers between 20 and 40}. 2. If Set A = {a,b,c}, Set B = {a,b,c,p,q,r}, U = {a,b,c,d,p,q,r,s}, find the following using sets formulas, a) A U B b) A ∩ B c) A' d) Is A
number less than 15} Rubrics: Accuracy: 20 points Participation: 15 points Presentation: 15 points Total Points: 50 points 8. Evaluating Learning
Test I Answer: 1. ∈
- {p}, {q}, {r},{p,q}, {q,r},{p,r},{p,q,r},∅ only 3-5. semantic notation, rooster notation, and set builder notation.
EVALUATE (8 minutes) Test I: Guess Me!
The teacher will read the questions twice. Students will write the correct answer to a ¼ sheet of paper.
The symbol used to denote an element of a set is ___.
Subsets of the set A = {p,q,r} are
What are the different set notations to represent set?
Additional Activities
EXTEND (2 minutes) Assignment: 1 Long Bondpaper Define what is set, types of sets and give each an example. IV. REMARKS V. REFLECTION
Prepared by: Angel P. Limbas– BSEd Math II
Limbas-Lesson Plan - This lesson plan is a 7Es semi-detailed. It's all about the Introduction of
Course: BSEd Mathematics (HOM-1)
University: JH Cerilles State College

- Discover more from: