- Information
- AI Chat
MATH6-Q1- Module 3
BSEd Mathematics (HOM-1)
JH Cerilles State College
Related documents
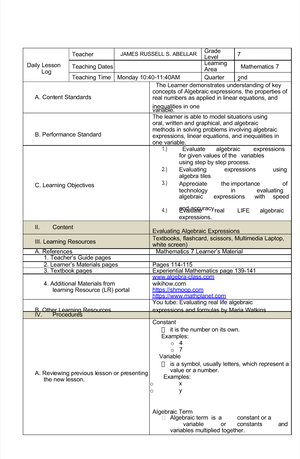
- Detailed- Lesson-PLAN Grade-9-MATH 084824
- New-lp - For educational purpose only.
- Dlp-m8al-ig-1-finds-the-equation-of-a-line-given-two-points-slope-and-a-point-and-slope-and-its-intercepts compress
- Lesson-plan-on-factoring-polynomial-with-common-monomial-factor compress
- Assure Model - Lesson plan
- Math-9-1st-summative
Preview text
Mathematics
Quarter 3 – Module 3:
Giving Translation of Real-Life Verbal
Expressions and Equations Into
Letters or Symbols and Vice Versa
6
Mathematics – Grade 6 Alternative Delivery Mode Quarter 3 – Module 3: Giving translation of real-life verbal expressions and equations into letters and symbols First Edition, 2020
Republic Act 8293, section 176 states that: No copyright shall subsist in any work of the Government of the Philippines. However, prior approval of the government agency or office wherein the work is created shall be necessary for exploitation of such work for profit. Such agency or office may, among other things, impose as a condition the payment of royalties.
Borrowed materials (i., songs, stories, poems, pictures, photos, brand names, trademarks, etc.) included in this book are owned by their respective copyright holders. Every effort has been exerted to locate and seek permission to use these materials from their respective copyright owners. The publisher and authors do not represent nor claim ownership over them.
Published by the Department of Education Secretary: Leonor Magtolis Briones Undersecretary: Diosdado M. San Antonio
Printed in the Philippines by ________________________ Department of Education – Region VI Office Address: Duran Street, Iloilo City Telefax: (033)336-2816, (033)509- E-mail Address: region6@deped.gov
Development Team of the Module Author: Robert S. Lapus Editors: Mae Joy M. Tan, Susana L. Lutero, Nora B. Rebadomia, Mary Jane O. Amante, Ma. Pinky C. Arquio, Susan T. Dela Torre, Ritchel P. Maratas Reviewers: Ivy Joy A. Torres, Ma. Theresa L. Tabotabo, Jem Rymon S. Chien Mae Joy M. Tan, Illustrators: Jerome Jordan Z. Ponsica, Eldiardo E. Dela Peňa Layout Artists: Jerome Jordan Z. Ponsica, Eldiardo E. Dela Peňa, Michael M. Jolo Management Team: Ramir B. Uytico Pedro T. Escobarte, Jr. Elena P. Gonzaga Donald T. Genine Adonis A. Mosquera Clarissa G. Zamora Fevi S. Fanco Ivy Joy A. Torres Jason R. Alpay Mae Joy M. Tan Jem Rymon S. Chien Ethel S. Gali
Introductory Message This Self-Learning Module (SLM) is prepared so that you, our dear learners, can continue your studies and learn while at home. Activities, questions, directions, exercises, and discussions are carefully stated for you to understand each lesson. Each SLM is composed of different parts. Each part shall guide you step-by- step as you discover and understand the lesson prepared for you. Pre-tests are provided to measure your prior knowledge on lessons in each SLM. This will tell you if you need to proceed on completing this module or if you need to ask your facilitator or your teacher’s assistance for better understanding of the lesson. At the end of each module, you need to answer the post-test to self- check your learning. Answer keys are provided for each activity and test. We trust that you will be honest in using these. In addition to the material in the main text, Notes to the Teacher are also provided to our facilitators and parents for strategies and reminders on how they can best help you on your home-based learning. Please use this module with care. Do not put unnecessary marks on any part of this SLM. Use a separate sheet of paper in answering the exercises and tests. And read the instructions carefully before performing each task. If you have any questions in using this SLM or any difficulty in answering the tasks in this module, do not hesitate to consult your teacher or facilitator. Thank you.
What I Need to Know This module was designed and written with you in mind. It is here to help you master the skills in translating real-life verbal expressions and equations into letters or symbols and vice versa. The scope of this module allows you to use it in many different learning situations. The language used recognizes your diverse vocabulary level. The lessons are arranged to follow the standard sequence of your course. But the order in which you read them can be changed to match with the textbook you are now using.
The module is divided into two lessons, namely: Lesson 1 – Translating real-life verbal expressions and equations into letters or symbols and vice versa Lesson 2 – Identifying a variable in an algebraic expression and equation
After going through this module, you are expected to:
- Translate real-life verbal expressions and equations into letters or symbols and vice versa (M6AL-IIIe-16) and
- Identify a variable in an algebraic expression and equation (M6AL-IIIe-17)
Lesson
1
Translating Real-life Verbal Expressions and Equations into Letters and Symbols and Vice Versa
In the previous lessons you have learned how to differentiates expression from equation. This time we will focus on translating real-life verbal expressions and equations into letters and vice versa.
What’s In
Translate the following algebraic expressions into word phrases. Write your answer in your answer sheet.
2 m + n
3 x – 7
5 + (2x)
2 (a + b)
6 x ÷ 2
n + 2m
Notes to the Teacher This contains helpful tips or strategies that will help you in guiding the learners.
What’s New Read and understand the problem below.
Mr. and Mrs. Romeo own a laundry shop. They have 152 customers this week, 24 fewer than last week. Write an algebraic equation for the number of customers they had last week.
What is It To translate the given problem into algebraic equation, consider this: Let m be the number they had last week. Translation: Twenty-four fewer than the number last week is 152 m – 24 = 152
Algebraic equation: m – 24 = 152 (The number of costumers last week is 24 fewer than m is 152)
Example 2: A kite is flying at an altitude of m meters. Express algebraically its new altitude after rising 20 meters. Translate: m meter is increased by 20
m + 20
Algebraic expression: m + 20 (The kite’s new altitude is 20 meters more than m meters)
What’s More A. Translate the following numerical expressions/equations into word phrases.
Numerical Expressions/Equations Translations
- 25 + y
- 5 n = 120
- 45k
- 2 r + 4 = 20
- t ÷ 6 = 130
B. Translate the following into numerical expression / equation. Write your answers on your answer sheet.
Twice the sum of 8 and r Translation: _________________________________
Mike weighs r pounds. Translate algebraically his weight after he gained 5 pounds. Translation: _________________________________
Billy is z years old now. Express his age 8 years ago. Translation: _________________________________ Refer inside the box for items 4-5.
Express Kris’ age algebraically Translation: _________________________________
Write the expression for the sum of Marivic’s and Roselyn’s ages. Translation: _________________________________
Marivic is thrice as old as Roselyn. If Roselyn is m years old, Kris is 3 years older than Roselyn.
What I Have Learned
To translate verbal expressions and equations into letters or symbols and vice versa, familiarity with words and phrases associated with symbols or operations are very important.
These are key words that might be useful in translating word phrase to mathematical symbols.
Symbols Meaning/s
####### + addition, plus, the sum of, more than, added to, increased by, thetotal of
- subtraction, minus, the difference of, less than, decreased by,diminished by, subtracted from, less, take away, fewer than x, • , ( ) multiplication, times, the product of, of, twice, multiplied by, thrice
####### ÷,/, ― division, divided by, the quotient of, the ratio of, per
####### = equals, is equal to, is, is the same as
Assessment
Match the word phrases in column A with the numerical expressions /equations in column B. Write the letter of the correct answer in your answer sheet. A B
a number b subtracted from 12 a. 6y
six times the number y b. 2x 2
the sum of five and thrice a number z c. 5 + 3z
twelve divided by n d. 6x - 5
one less than the product of 4 and y e. 9k
a number z increased by ten f. z + 10
twice the square of a number x g. 3 (4r)
thrice the product of 4 and r h. 4y - 1
nine times a number k i. 12 - b
six times a number x minus five j. 12 ÷ n
Additional Activities
A. Translate the following verbal phrases into algebraic expressions or equations:
- five subtracted from twice z
- a number p less eleven is fifty
- fifteen decreased by a number p
- the square of the product of x and y
- the sum of six and twenty less five equals the number z
B. Translate the following numerical expressions/equations into word phrases:
- 2 x + 5
- 5 x – 8
- 4 (y + 7)
- 2 n = 120
- 42 = 16
In the previous lessons you have learned to translate real-life verbal expressions and equations into letters and vice versa. This time, we will focus on identifying a variable in an algebraic expression and equation.
A. Identify the number that should replace the question mark to make the mathematical statement correct. Write your answers on your answer sheet.
1.? + 5= 22 2. 72 ÷? = 8 3. 19 =? – 12 4. 7+2= 3+? 5. 21 x? = 63
B. Translate the following word phrases into algebraic expression and identify the variable(s). Write your answer on your answer sheet.
- Five times the sum of a and b
- Twelve decreased by twice x
- Fifty-one minus the product of r and five
- Seven is multiplied to the difference of two and x
- The quotient of twelve and four added to x
Lesson
2
Identifying a Variable in an
Algebraic Expression and
Equation
What’s In
Read and analyze the problem. Leni bought 5 apples which cost ₱12 each. She gave the seller a ₱100. bill. How much change did Leni receive?
- What did Leni buy?
- How much did she give to the seller?
- What do you need to find out?
- What is used to represent unknown number?
To solve a mathematical problem, the variable is used to represent unknown number. A variable is any letter or symbol that represents a number.
To solve the above problem, let us use variables to represent the unknown numbers. Let: y = be the cost of apples z = be the change that Leni received from her ₱100 bill To find the cost of apples, we use this equation: 5 x ₱12 = y Solution: 5 x ₱12 = y P60 = y To find the change Leni received, we use this equation: ₱100 – ₱60 = z Solution: ₱100 – ₱60 = z ₱40 = z Therefore, Leni received ₱40 change from her ₱100 bill.
What’s New
What is It
What I Have Learned
An algebraic expression is a mathematical phrase that uses variables, numerals, and operation symbols.
Any letter or symbol used to represent a number in an algebraic expression or equation is called a variable.
Translate the following word phrases into an algebraic expression or equation. Use a variable to represent an unknown number. Write your answer on your answer sheet.
- fifteen is subtracted from the quotient of a and b.
- a number diminished by seven
- four greater than two times a number is equal to sixty.
- the sum of a number and six is forty.
- thrice a number decreased by twenty
- the square of a number is sixteen
- the quotient of twice a number and five
- twice a number increased by five is thirty-seven
- a number divided by two
- the difference between ten times a number and twelve
What I Can Do
Assessment
Write the variables used in each item below. Write the correct answer in your answer sheet.
- 37 – ( 3 + y )
- 5 ( 4 – b )
- y = 2 + 46
- n = 24 x 2
- z x 9 = 90 ÷ 10
- forty divided by p
- r less than a product of two and eight
- eighteen less than x
- q less than the product of six and for is eighteen
- the sum of t and fifty-seven is sixty-five
MATH6-Q1- Module 3
Course: BSEd Mathematics (HOM-1)
University: JH Cerilles State College

- Discover more from:
Recommended for you
Students also viewed
Related documents
- Detailed- Lesson-PLAN Grade-9-MATH 084824
- New-lp - For educational purpose only.
- Dlp-m8al-ig-1-finds-the-equation-of-a-line-given-two-points-slope-and-a-point-and-slope-and-its-intercepts compress
- Lesson-plan-on-factoring-polynomial-with-common-monomial-factor compress
- Assure Model - Lesson plan
- Math-9-1st-summative