- Information
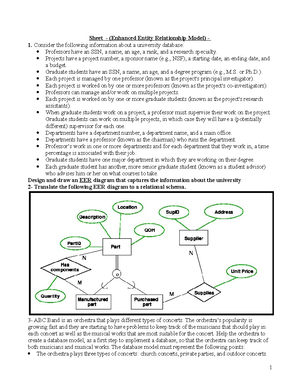
- AI Chat
Data Mining - Ch7 Cluster Lecture 2
Major Clustering Approaches, Typical Alternatives to Calculate the Dis...
Course
Data Mining
91 Documents
Students shared 91 documents in this course
University
Assiut University
Academic year: 2023/2024
Listed bookData Mining: Concepts and Techniques
Uploaded by:
531Uploads
415upvotes
Recommended for you
Preview text
Data Mining Concepts
CH7 - Lecture 2 : Cluster Analysis II
TOPICS
1. What is Cluster Analysis?
2. Types of Data in Cluster Analysis
3. A Categorization of Major Clustering
Methods
4. Partitioning Methods
5. Hierarchical Methods
6. Density-Based Methods
7. Grid-Based Methods
8. Model-Based Methods
9. Clustering High-Dimensional Data
10. Constraint-Based Clustering
11. Outlier Analysis
12. Summary
- A model is hypothesized for each of the
####### clusters and tries to find the best fit of that
####### model to each other
- Typical methods: EM, SOM, COBWEB
- Frequent pattern-based:
- Based on the analysis of frequent patterns
- Typical methods: pCluster
- User-guided or constraint-based:
- Clustering by considering user-specified or
####### application-specific constraints
- Typical methods: COD (obstacles),
####### constrained clustering
Typical Alternatives to
Calculate the Distance
between Clusters
- Single link: smallest distance between an
element in one cluster and an element in
the other, i., dis(Ki, Kj) = min(tip, tjq)
- Complete link: largest distance between
an element in one cluster and an element
in the other, i., dis(Ki, Kj) = max(tip, tjq)
- Average: avg distance between an element
in one cluster and an element in the other,
i., dis(Ki, Kj) = avg(tip, tjq)
- Centroid: distance between the centroids of
two clusters, i., dis(Ki, Kj) = dis(Ci, Cj)
- Medoid: distance between the medoids of
two clusters, i., dis(Ki, Kj) = dis(Mi, Mj)
- Medoid: one chosen, centrally located
object in the cluster
Partitioning Methods
Partitioning Algorithms: Basic
Concept
- Partitioning method: Construct a partition of a
database D of n objects into a set of k
clusters, s., min sum of squared distance
- Given a k, find a partition of k clusters that
optimizes the chosen partitioning criterion
- Global optimal: exhaustively enumerate
all partitions
- Heuristic methods: k-means and k-
medoids algorithms
- k-means (MacQueen’67): Each cluster is
represented by the center of the cluster
- k-medoids or PAM (Partition around
medoids) (Kaufman & Rousseeuw’87):
Each cluster is represented by one of
the objects in the cluster
The K-Means Clustering
Method
- Given k, the k-means algorithm is
implemented in four steps:
- Partition objects into k nonempty
subsets
- Compute seed points as the
centroids of the clusters of the
current partition (the centroid is
the center, i., mean point, of the
cluster)
- Assign each object to the cluster
with the nearest seed point
- Go back to Step 2, stop when no
more new assignment
- Weakness
- Applicable only when mean is defined,
then what about categorical data?
- Need to specify k, the number of clusters,
in advance
- Unable to handle noisy data and outliers
- Not suitable to discover clusters with non-
convex shapes
Variations of the K-Means
Method
- A few variants of the k-means which differ in
- Selection of the initial k means
- Dissimilarity calculations
- Strategies to calculate cluster means
- Handling categorical data: k-modes
(Huang’98)
- Replacing means of clusters with modes
- Using new dissimilarity measures to deal
with categorical objects
- Using a frequency-based method to
update modes of clusters
- A mixture of categorical and numerical
data: k-prototype method
- Find representative objects, called medoids,
in clusters
- PAM (Partitioning Around Medoids, 1987)
- starts from an initial set of medoids and
iteratively replaces one of the medoids
by one of the non-medoids if it improves
the total distance of the resulting
clustering
- PAM works effectively for small data sets,
but does not scale well for large data
sets
- CLARA (Kaufmann & Rousseeuw, 1990)
- CLARANS (Ng & Han, 1994): Randomized
sampling
- Focusing + spatial data structure (Ester et al.,
1995)
A Typical K-Medoids
Algorithm (PAM)
- repeat steps 2-3 until there is no
change
PAM Clustering: Total
swapping cost TCih= åjCjih
What Is the Problem with
PAM?
- Pam is more robust than k-means in
the presence of noise and outliers
because a medoid is less influenced
by outliers or other extreme values
than a mean
- Pam works efficiently for small data
sets but does not scale well for
large data sets.
- O(k(n-k)
2
) for each iteration
where n is # of data,k is # of
clusters
èSampling based method,
CLARA(Clustering LARge
Applications)
the whole data set if the sample
is biased
CLARANS (“Randomized”
CLARA) (1994)
- CLARANS (A Clustering Algorithm
based on Randomized Search) (Ng
and Han’94)
- CLARANS draws sample of
neighbors dynamically
- The clustering process can be
presented as searching a graph
where every node is a potential
solution, that is, a set of k medoids
- If the local optimum is found,
CLARANS starts with new randomly
selected node in search for a new
local optimum
- It is more efficient and scalable than
both PAM and CLARA
- Focusing techniques and spatial
access structures may further
improve its performance (Ester et
al.’95)
Was this document helpful?
Data Mining - Ch7 Cluster Lecture 2
Course: Data Mining
91 Documents
Students shared 91 documents in this course
University: Assiut University
Was this document helpful?

Data Mining Concepts
CH7 - Lecture 2 : Cluster Analysis II
Data Mining - Chapter 7
1
Too long to read on your phone? Save to read later on your computer
Discover more from:
Data Mining
Assiut University
91 Documents
- Discover more from:Data MiningAssiut University91 Documents
More from:Data Mining
More from:
Data Mining
Assiut University
91 Documents
- More from:Data MiningAssiut University91 Documents